2.24

核密度估计

通过一个知乎回答学习了核密度估计（Kernel density estimation，KDE），能够用样本估计概率密度函数。

可以通过一个简单的 python 程序展示 KDE 的效果（使用高斯核函数）：

import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats

dataAmount = 10 ** 5
xAmount = 10 ** 4
data = np.random.uniform(-10, 10, dataAmount)
x = np.linspace(-10, 10, xAmount)
kde = stats.gaussian_kde(data)
density = kde(x)

plt.plot(x, density)
plt.show()

输出如下：
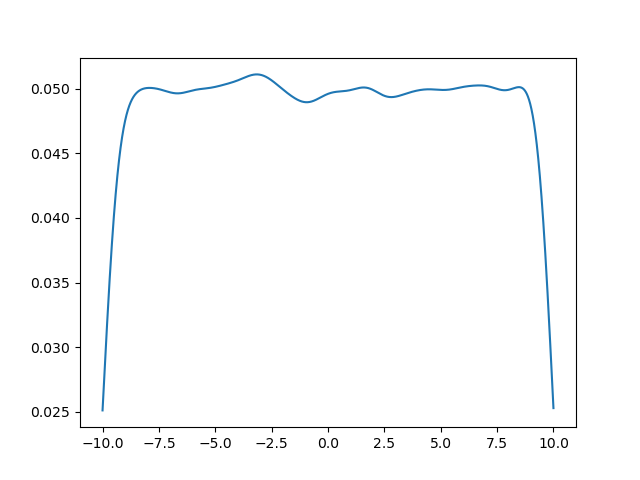
KDE example.png
极限的理想情况是在中间呈现均匀分布，但 dataAmount 和 xAmount 都有限，我们希望在相同计算量的情况下达到最好的效果。

计算量

对于计算量，从 KDE 公式上看，复杂度应该是 dataAmount * xAmount ，但测试发现并非如此：

startTime = time.perf_counter()

def startCount():
    global startTime
    startTime = time.perf_counter()

def printTime(x:str):
    global startTime
    print(x + ": " + (time.perf_counter() - startTime).__str__())
    startTime = time.perf_counter()
    
for i in range(5, 9):
    j = 9 - i
    dataAmount = 10 ** i
    xAmount = 10 ** j
    data = np.random.uniform(-10, 10, dataAmount)
    x = np.linspace(-10, 10, xAmount)
    startCount()
    kde = stats.gaussian_kde(data)
    kde(x)
    printTime("data amount = {}, xAmount = {}".format(dataAmount, xAmount))

输出：

data amount = 100000, xAmount = 10000: 5.868209599982947
data amount = 1000000, xAmount = 1000: 8.375833499943838
data amount = 10000000, xAmount = 100: 12.967822499922477
data amount = 100000000, xAmount = 10: 20.36547399999108

进一步实验：

results = np.full((10, 10), np.nan)
for i in range(1, 10):
    for j in range(1, 11 - i):
        dataAmount = 10 ** i
        xAmount = 10 ** j
        data = np.random.uniform(-10, 10, dataAmount)
        x = np.linspace(-10, 10, xAmount)
        startCount()
        kde = stats.gaussian_kde(data)
        kde(x)
        results[i][j] = time.perf_counter() - startTime

df = pd.DataFrame(results)
df.drop(columns=[0], index=[0], inplace=True)
print(df.to_string(na_rep=''))

输出：

	1	2	3	4	5	6	7	8	9
1	0.032673	0.000223	0.00274	0.001742	0.006912	0.063041	0.632997	6.311374	78.66403
2	0.021071	0.000292	0.003947	0.006638	0.068121	0.605103	5.983759	60.18651
3	0.000999	0.001523	0.006448	0.060406	0.584952	5.902063	58.92799
4	0.003021	0.006319	0.057359	0.577309	5.777679	58.72213
5	0.008281	0.064728	0.584895	5.897568	59.1081
6	0.124268	0.879937	8.686681	84.32257
7	1.678993	12.47852	123.3277
8	19.62004	156.6667
9	361.3757

可以看出， $\log t i m e$ 关于 dataAmount 相比关于 XAmount 的增长实际上更快

视觉效果

def generate_kde(i, j):
    dataAmount = 10 ** i
    xAmount = 10 ** j
    data = np.random.uniform(-10, 10, dataAmount)
    x = np.linspace(-10, 10, xAmount)
    kde = stats.gaussian_kde(data)
    return (x, kde(x))

  

rows, cols = 8, 8
fig, axes = plt.subplots(rows, cols, figsize=(11, 11))

for i in range(rows):
    for j in range(cols):
        if (i + j >= 8):
            axes[i, j].axis('off')
            
        else:
            ax = axes[i, j]
            ax.set_xticks([])
            ax.set_yticks([])
            x, kde = generate_kde(i + 1, j + 1)
            ax.plot(x, kde)
            ax.set_title(f'({i + 1},{j + 1})')

plt.show()

可以看出，dataAmount 比 XAmount 的作用大得多！