2.19

广义傅里叶变换

经典的傅里叶变换完全不能处理 狄拉克 δ 函数，三角函数，也不能良好地处理矩形函数这样的不连续函数。所以需要一种广义傅里叶变换来处理更多函数。广义傅里叶变换依赖分布的概念，在定义了分布之后，给出傅里叶变换的定义是完全自然的。EE 261 的 Lecture 11 - Lecture 14 都在讲述广义傅里叶变换的故事。

注意，这里的分布与概率论意义的分布不相同，它不是一个函数，而是线性泛函。分布是广义的函数。一个分布完全等同于它在测试函数上的作用效果，正如人是其社会关系的总和。这就是说，我们通过直接考察作用效果而抛弃了函数的概念本身，这使得接纳那些作用明确但难以良定义的“函数”成为可能。

一个逻辑问题

大物实验绪论课上，出现了这样一个逻辑问题：

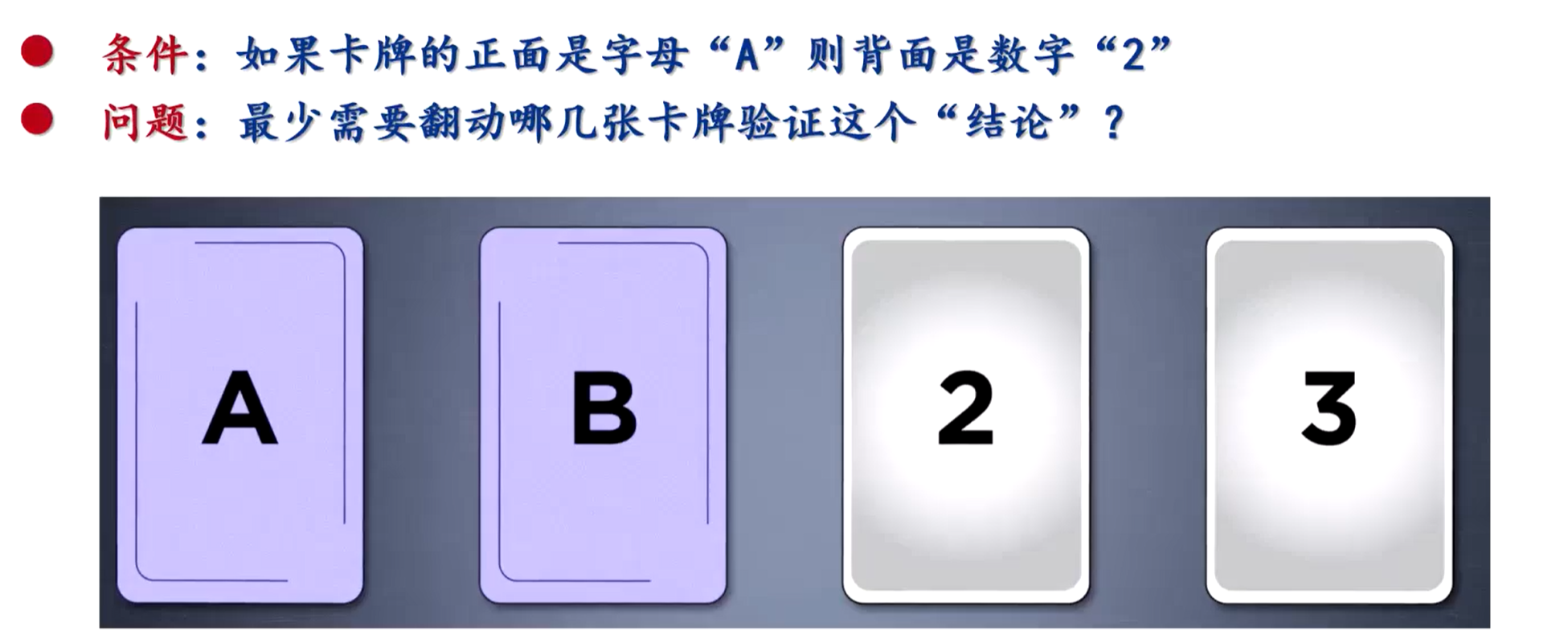
大物实验绪论1.png

一共提交了 292 份问卷，答案分布如下：

大物实验绪论2.png
令人忍俊不禁

学习规划

目前傅里叶变换学到采样定理的应用，还将持续两节课（Lecture 18 - Lecture 19），然后是离散傅里叶变换（DFT）和线性时不变系统。线性时不变系统可能对电路理论学习有所帮助，但总体而言，继续学习该课程不是最优的选择。目前有三个问题需要平衡：课内学习，AI 学习，CS 课程学习，需要仔细考虑时间分配问题。

课内方面，英语期末考试在第 13 周，从上学期期末看，听力是弱项，即使是炸鱼分段的大英二，课上的听力填空对我而言也很有难度。固然，依靠无字幕听课+适当倍速可以提供常态化的听力环境，但针对性的听力填空训练也是必要的。除了英语，其他课程听课+考前复习都可以速通。
AI 学习需要先补足数学基础。根据 ChatGPT 分析，我还需要学习的包括线性代数中的 SVD 分解等内容；概率论；信息论。线代可以学习 MIT 18.06 的 Chapter 7, Chapter 9；概率论准备自学茆诗松的教材；信息论暂定跟课 MIT6.050J 。所以计划是先速通线代，然后平时课上看书学概率论，空闲时间上信息论。补完数学基础后，就是 Deep Learning 和 NLP 基础，ChatGPT 也给出了一些建议，暂时不仔细研究。
CS 课程学习不得不暂时搁置。这意味着 CSAPP 的 shlab 要拖到挺久之后完成。之后还会学习虚拟内存一节，最后的网络编程和并行编程就暂时跳过，留给更专门化的课程学习。

递归学习不适用于数学

如题，数学学习需要良好的引导，这包括：

把知识用自然的顺序组织起来。以 EE261 为例，先讲傅里叶级数，再讲傅里叶变换，得到傅里叶变换的过程非常自然
明确目前在做什么，即良好的 motivation，以 EE261 为例，Lecture 11 明确了这一个阶段的目的是对更多函数建立傅里叶变换，一个子目标是找到一个函数集合，傅里叶变换在其上有良好的性质。
对涉及的数学证明进行取舍。以 EE261 为例，舍弃了大量困难的推导，保留了能带来 insight 的，并且相对容易的那些推导。
过滤错误信息。这是显然的，互联网上的信息良莠不齐，你能够在 CSDN 或知乎等平台上找到的数学内容，其正确性不能得到保证，但 Wikipedia 并未很多地考虑可读性，所以陷入了难题。你不会希望对于每个问题，阅读原始的数学论文。
使用一致的体系。体系有多重含义：可以是说使用的那套数学符号，也可以是归一化的方式。傅里叶变换本身就需要归一化，遵循一套一致的归一化体系能极大减少思维负担。

当然还有很多，但仅仅是以上五点，就是利用互联网递归学习难以做到的。对于记忆空间并非无限大的人类，另一个危险是爆栈